矩阵树定理
外观
此條目翻譯品質不佳。 (2021年4月7日) |
在图论中,矩阵树定理(matrix tree theorem)或基尔霍夫定理(Kirchhoff theorem)是指图的生成树数量等于调和矩阵的余子式(所以可以在多项式时间内计算)。
若 G 有 n 个顶点,λ1, λ2, ..., λn-1 是拉普拉斯矩阵的非零特征值,则
这个定理以古斯塔夫·基爾霍夫名字命名。 这也是凯莱公式的推广(若图是完全图)。
举例
[编辑]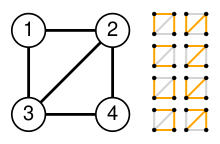
对于右图的例子,首先求出调和矩阵 :
随后求出余子式,也即删除任何一个行和一个列,例如第一行和第一列:
则
.
完全图 Kn 的调和矩阵是
任何餘因子的行列式是 nn-2 。再说L的所有特征值是n,而且L只有n-1个特征向量。所以生成树的总数又是 nn-2 。
证明大纲
[编辑]拉氏矩阵有这个属性:任何行或列的元素总和等于0。所以,无论删除什么行或列,都是不变的。或者说L的任何餘因子有同样的行列式。
若是接续矩阵,则拉普拉斯矩阵 。在矩阵中,删除任何一个行或列得到矩阵,那么,其中 表示 删除第一行第一列后得到的余因子矩阵。
可以表示这个行列式给予生成树的数量。
参见
[编辑]阅读
[编辑]- Harris, John M.; Hirst, Jeffry L.; Mossinghoff, Michael J., Combinatorics and Graph Theory, Undergraduate Texts in Mathematics 2nd, Springer, 2008
- Maurer, Stephen B., Matrix generalizations of some theorems on trees, cycles and cocycles in graphs, SIAM Journal on Applied Mathematics, 1976, 30 (1): 143–148, MR 0392635, doi:10.1137/0130017.
- Tutte, W. T., Graph Theory, Cambridge University Press: 138, 2001, ISBN 978-0-521-79489-3.
- Chaiken, S.; Kleitman, D., Matrix Tree Theorems, Journal of Combinatorial Theory, Series A, 1978, 24 (3): 377–381, ISSN 0097-3165, doi:10.1016/0097-3165(78)90067-5
参考文献
[编辑]- ^ Graphs, Matrices, Isomorphism. math.fau.edu. [2020-02-14]. (原始内容存档于2009-03-04).



![{\displaystyle Q=\left[{\begin{array}{rrrr}2&-1&-1&0\\-1&3&-1&-1\\-1&-1&3&-1\\0&-1&-1&2\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/578516027c122e4b3fb198bc7cc830acc2d8342b)
![{\displaystyle Q^{\ast }=\left[{\begin{array}{rrr}3&-1&-1\\-1&3&-1\\-1&-1&2\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f4e0948fbaaf312ad9993e2a3054b9bb7d606ac)









