阿特伍德機
外观
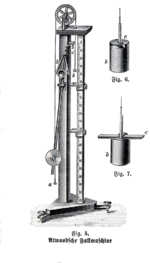
阿特伍德機(Atwood machine,又譯作阿特午德機或阿特午機),是由英國牧師、數學家兼物理學家的乔治·阿特伍德在1784年发表的《关于物体的直线运动和转动》一文中提出的[1],用於測量加速度及驗證運動定律的機械。此機械現在經常出現於學校教學中,用來解釋经典物理學的原理,验证力學中做恒定加速度运动的运动规律。
一個理想的阿特伍德機包含兩個物體質量m1和m2,及由無重量、無彈性的繩子連結並包覆理想且無重量的滑輪。 [2]
當,无论兩物體在何位置、機器處於力平衡的狀態。當时,兩物體皆以大小相等的加速度做运动。
恆定加速度的方程式
[编辑]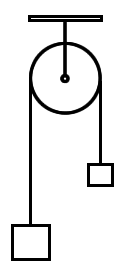
我們可以藉由分解力的方法得到一個加速度的方程式。如果繩子無重量、無彈性,滑輪理想(無視半徑)且無重量,那麼我們只需要考慮張力(T),還有兩個物體的重量(mg)。先找出個別影響兩物體的力,當时,
m1的力:
m2的力:
利用牛頓第二運動定律, , 。 将这两个方程式相加, 我們可以得到整個系統的恒定的加速度的方程式。定义合力, 我们有 。
阿特伍德機有時候也被用來說明拉格朗日力學中獲得的運動方程式。 [3]
计算張力的方程式
[编辑]上述的方程式也可用來計算繩子上的張力,只需要將得到的等加速度方程式代入兩物體的力方程式之一中。
例如代入,我們得到
藉由同樣的方法,張力也可以從中求得。
有轉動慣量滑輪和摩擦存在的情况
[编辑]若m1與m2之間的重量差别很小時,半徑为(r)的滑輪的轉動慣量(I)不可以被忽略。当不打滑时,滑輪的角加速度可以從以下算式求得:
在此情況下,作用于滑輪上的總力矩為:
把该方程式与两个垂吊物体的方程式 , 联合求解 , 和 ,我们得到:
參考
[编辑]- ^ 漆安慎、杜婵英. 《力学》(第二版). 高等教育出版社. 2005: 76页. ISBN 978-7-04-016624-8.
- ^ Tipler, Paul A. Physics For Scientists and Engineers, Third Edition, Extended Version. New York: Worth Publishers. 1991. ISBN 0-87901-432-6. Chapter 6, example 6-13, page 160.
- ^ Goldstein, Herbert. Classical Mechanics, second Edition. New Delhi: Addison-Wesley/Narosa Indian Student Edition. 1980. ISBN 81-85015-53-8. Section 1-6, example 2, pages 26-27.
- "Atwood's Machine (页面存档备份,存于互联网档案馆)" by Enrique Zeleny, The Wolfram Demonstrations Project.
- "Spreading Newtonian Philosophy with Instruments: The Case of Atwood's Machine". Http://dx.doi.org/10.4236/ahs.2014.31007


























