三角函數線
外觀
三角函數線是正弦線、餘弦線和正切線的總稱,是三角函數的幾何表示。

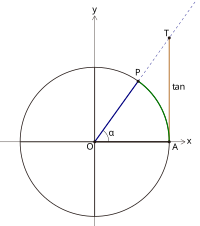
由於,與點P(x, y)在終邊上的位置無關,為簡單起見,選取角α的終邊 與單位圓的交點為P(x, y),則sin α = y, cos α = x。
過點P作x軸的垂線,垂足為M,顯然,線段OM的長度為 |x|,為了去掉絕對值符號,我們引入有向線段的概念[1]。
有向線段
[編輯]規定了方向(起點和終點)的線段稱為有向線段(與向量有區別),類似地可以把規定了正方向的直線稱為有向直線。若有向線段AB在有向直線l上或與有向直線l平行,根據有向線段AB與有向直線l的方向相同或相反,分別把它的長度添上正號或負號,這樣所得的數,叫做有向線段的數量,記為AB。
正弦線和餘弦線
[編輯]引入有向線段的概念後,如果x > 0,如圖,有向線段OM與x軸同向,其數量為x,如果x < 0,有向線段OM與x軸反向,其數量也為x,故總有OM = x。同理可知MP = y
所以有,sin α = MP, cos α = OM
即有向線段MP、OM的數量分別等於α的正弦、α的餘弦。因此,我們把有向線段MP,OM分別叫作角α的正弦線、餘弦線。
正切線
[編輯]當角α的終邊在y軸的右側時(如左圖),在角α的終邊上取點T(1, y'),則(A為單位圓與x軸正半軸的交點)
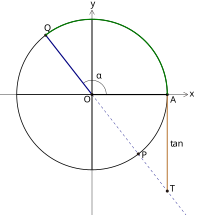
當角α終邊在y軸左側時(如右圖),在角α的終邊的反向延長線上取點T(1, y')由於它關於原點的對稱點Q(−1, −y')在角α的終邊上,故有
即總有tan α = AT
因此,我們把有向線段AT叫做角α的正切線
參考資料
[編輯]- ^ 《数学 必修4》. 江蘇教育出版社. : 12~13. ISBN 978-7-5343-6225-5 (中文(簡體)).