導數

  提示：此條目頁的主題不是倒數。

一個實值函數的圖像曲線。函數在一點的導數等於它的圖像上這一點處之切線的斜率。

導數（英語：derivative）是微積分學中的一個概念。函數在某一點的導數是指這個函數在這一點附近的變化率（即函數在這一點的切線斜率）。導數的本質是通過極限的概念對函數進行局部的線性逼近。當函數$f$的自變量在一點$x_{0}$上產生一個增量$h$時，函數輸出值的增量與自變量增量$h$的比值在$h$趨於0時的極限如果存在，即為$f$在$x_{0}$處的導數，記作$f'(x_{0})$、${\frac {\mathrm {d} f}{\mathrm {d} x}}(x_{0})$或$\left.{\frac {\mathrm {d} f}{\mathrm {d} x}}\right|_{x=x_{0}}$。例如在運動學中，物體的位移對於時間的導數就是物體的瞬時速度。

導數是函數的局部性質。不是所有的函數都有導數，一個函數也不一定在所有的點上都有導數。若某函數在某一點導數存在，則稱其在這一點可導(可微分)，否則稱為不可導(不可微分)。如果函數的自變量和取值都是實數的話，那麼函數在某一點的導數就是該函數所代表的曲線在這一點上的切線斜率。

對於可導的函數$f$，$x\mapsto f'(x)$也是一個函數，稱作$f$的導函數。尋找已知的函數在某點的導數或其導函數的過程稱為求導（英語：differentiation）。反之，已知導函數也可以倒過來求原來的函數，即不定積分。微積分基本定理說明了求原函數與積分是等價的。求導和積分是一對互逆的操作，它們都是微積分學中最為基礎的概念。

定義

一般定義

一個動畫，給出了一個直觀的導數概念，因為參數變化時函數的「擺動」會改變。

直觀上 $f(x)-f(a)$代表函數值從 $a$ 到 $x$ 的變化量，那這樣，

${\frac {f(x)-f(a)}{x-a}}$

代表的是從 $a$ 到 $x$ 的平均變化率，如果把 $x$ 趨近於 $a$，似乎就可以更能貼切的描述函數值在 $a$ 附近的變化。

以此為動機，若實函數 $f$ 於實數 $a$ 有定義，且以下極限（注意這個表達式所定義的函數定義域不含 $a$ ）

$\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}$

存在則稱 $f$ 於 $a$ 處可導，並稱這個極限為 $f$ 於 $a$ 處的導數，記為$f^{\prime }(a)$也可記作 $\left.{\frac {\mathrm {d} f}{\mathrm {d} x}}\right|_{x=a}$ 或 ${\frac {\mathrm {d} f}{\mathrm {d} x}}(a)$ 。

根據函數極限的定義，導數定義部分的 ＂存在 $\delta >0$ 使所有的 $x\in D_{f}$ ，只要 $0<|x-a|<\delta$ 都有....＂ 可以直觀的理解為 ＂當 $h=x-a$ 趨近於 $0$ 都有....＂，但要把它寫成嚴謹的定義，會碰到 ＂存在 $\delta >0$ 對所有的實數 $h$ ，只要 $a+h\in D_{f}$ 且 $0<|h|<\delta$ 都有....＂這段敘述無法直接套入極限定義的問題，對此必須把以下的表達式

$\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}$

定義為導數原始極限表達式的簡記，而非另一種自動合法的導數定義。但如果存在 $r>0$ ，使 $f$ 在 $(a-r,\,a+r)$ 裏都有定義，那定義 $F$ 為以

$\{h\in \mathbb {R} \,|\,(h\neq 0)\wedge (|h|<r)\}$

為定義域，然後以

$F(h)={\frac {f(a+h)-f(a)}{h}}$

為對應規則的函數，那以下的極限式

$\lim _{h\to 0}F(h)=f^{\prime }(a)$

就可以把以 $h$ 為自變量的偏差，將之趨近於零求導數的想法納入正式的運算裏。

幾何意義

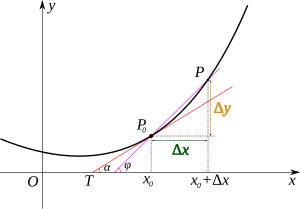
當函數定義域和取值都在實數域中的時候，導數可以表示函數的曲線上的切線斜率。如右圖所示，設$P_{0}$為曲線上的一個定點，$P$為曲線上的一個動點。當$P$沿曲線逐漸趨向於點$P_{0}$時，並且割線$PP_{0}$的極限位置$P_{0}T$存在，則稱$P_{0}T$為曲線在$P_{0}$處的切線。

若曲線為一函數$y=f(x)$的圖像，那麼割線$PP_{0}$（粉紅色）的斜率為：

$\tan \varphi ={\frac {\Delta y}{\Delta x}}={\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}$

當$P_{0}$處的切線$P_{0}T$（橘紅色），即$PP_{0}$的極限位置存在時，此時$\Delta x\to 0$，$\varphi \to \alpha$，則$P_{0}T$的斜率$\tan \alpha$為：

$\tan \alpha =\lim _{\Delta x\to 0}\tan \varphi =\lim _{\Delta x\to 0}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}$

上式與一般定義中的導數定義完全相同，也就是說$f'(x_{0})=\tan \alpha$，因此，導數的幾何意義即曲線$y=f(x)$在點$P_{0}(x_{0},f(x_{0}))$處切線的斜率。

導數、導函數與微分算子

主條目：微分算子

若函數 $\;f(x)\;$ 在其定義域包含的某區間 $\;I\;$ 內每一個點都可導，那麼也可以說函數$\;f(x)\;$ 在區間 $\;I\;$ 內可導，這時對於 $\;I\;$ 內每一個確定的$\;x\;$ 值，都對應着 $\;f\;$ 的一個確定的導數值，如此一來就構成了一個新的函數$x\mapsto f'(x)$，這個函數稱作原來函數 $\;f(x)\;$ 的導函數，記作：$\;y'\;$、$f'(x)\;$ 或者 ${\tfrac {\mathrm {d} f}{\mathrm {d} x}}(x)$。值得注意的是，導數是一個數，是指函數 $f(x)\;$ 在點 $x_{0}\;$ 處導函數的函數值。但在不至於混淆的情況下，通常也可以說導函數為導數。

由於對每一個可導的函數 $\;f(x)\;$，都有它的導函數 $f'(x)\;$ 存在，我們還可以定義將函數映射到其導函數的算子。這個算子稱為微分算子，一般記作 $D$ 或 ${\tfrac {\mathrm {d} }{\mathrm {d} x}}$。例如：

${\begin{aligned}D(x\mapsto 1)&=(x\mapsto 0)\\D(x\mapsto x)&=(x\mapsto 1)\\D(x\mapsto x^{2})&=(x\mapsto 2\cdot x)\end{aligned}}$

由於微分算子的輸出值仍然是函數，可以繼續求出它在某一點的取值。比如說對於函數 $\;f(x)=x^{2}\;$，

$D(f)=(x\mapsto 2\cdot x)$

所以$D(f)(x)=2x$，$D(f)(1.4)=2\times 1.4=2.8$。

導數與微分

微分也是一種線性描述函數在一點附近變化的方式。微分和導數是兩個不同的概念。但是，對一元函數來說，可微與可導是完全等價的。可微的函數，其微分等於導數乘以自變量的微分$\mathrm {d} x$，換句話說，函數的微分與自變量的微分之商等於該函數的導數。因此，導數也叫做微商。函數$y=f(x)$的微分又可記作$\mathrm {d} y=f'(x)\mathrm {d} x$。

歷史

主條目：微積分學 § 歷史

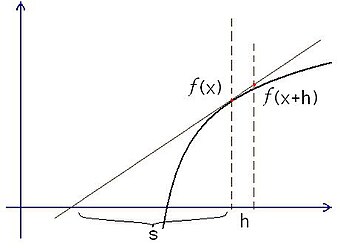
導數和積分的發現是微積分發明的關鍵一步。17世紀以來，光學透鏡的設計以及炮彈彈道軌跡的計算促使歐洲的數學家對曲線的切線進行研究。1630年代，法國數學家吉爾·德·羅伯瓦爾作出了最初的嘗試。與此同時，同是法國人的費馬在計算切線時已經使用了無窮小量的概念。

如右圖，費馬考慮曲線 $f(x)$ 在 $x$ 處的切線。他聲稱，對於切線，有以下的關係成立：

${\frac {s}{s+h}}={\frac {f(x)}{f(x+h)}}$

對上式變形後得到：

$s={\frac {f(x)}{\frac {f(x+h)-f(x)}{h}}}$

對於具體的函數 $f(x)$，比如 $f(x)=x^{3}$，費馬計算 ${\frac {f(x+h)-f(x)}{h}}$ 的值，並將 $h$設為0，就得到 $s$，從而確定切線的斜率。可以看出，費馬的方法實質上已經是求導。費馬還給出了 $f(x)$ 為多項式時切線的公式。英國的巴羅、荷蘭的於德（Johnann Van Waveren Hudde）和瓦隆的斯盧茲（René Francoiss Walther de Sluze）繼續了費馬的工作。然而，費馬和巴羅等人並沒有將求導歸納為一種獨立的工具，只是給出了具體的計算技巧。

1660年代，英國人伊薩克·牛頓提出了「流數」的概念。牛頓在寫於1671年的《流數法與無窮級數》中對流數的解釋是：「我把時間看作是連續的流動或增長，而其他的量則隨着時間而連續增長。我從時間流動性出發，把所有其他量的增長速度稱為流數。」也就是說，流數就是導數。牛頓將無窮小的時間間隔定義為「瞬間」（moment），而一個量的增量則是流數與瞬間的乘積。求導數時，牛頓將自變量和應變量兩邊展開，同時除以瞬間，再將剩下的項中含有瞬間的項忽略掉。而在他的第三篇微積分論文中，牛頓使用了新的概念：最初比和最後比。他說：

“ 隨我們的意願，流數可以任意地接近於在儘可能小的等間隔時段中產生的增量，精確地說，它們是最初增量的最初的比，它們也能用和它們成比例的任何線段來表示。 ”

相比於牛頓，德國數學家萊布尼茲使用了更清晰的記號來描述導數（見導數的記法一節）。他利用了巴羅的「微分三角形」概念，將自變量和應變量的增量記為 $dx$ 和 $dy$。他把 $dx$ 理解為「比任何給定的長度都要小」，而 $dy$ 則是 $x$ 移動時 $y$「瞬刻的增長」。而導數則是兩者之間的比例。他還研究了函數之和、差、積、商的求導法則。

伊薩克·牛頓爵士

牛頓和萊布尼茲的差別在於，牛頓將無窮小量作為求流數或導數的工具，而萊布尼茲則用無窮小量的比值來表示導數。這與二人的哲學思想差異有關。

微積分的理論面世後，遭到了有關無窮小量定義的攻擊與質疑。導數的定義自然也包括在內。萊布尼茲和牛頓對無窮小量的認識都是模糊的。不僅如此，萊布尼茲甚至引入了$(d)x$ 和 $(d)y$，稱其為「未消失的量」，用以進行求導前部的計算。在完成計算後再用「消失的量」$dx$ 和 $dy$來代替它們，並假定前兩者之比等於後兩者之比，認為這是一個不容置疑的真理。

許多數學家，包括伯努利兄弟、泰勒、麥克勞林、達朗貝爾、拉格朗日和歐拉都想要對微積分的嚴密性辯護或將微積分嚴密化。但受限於對無窮小量的認識，十八世紀的數學家並沒有做出太大的成果。微積分的強烈抨擊者，英國的喬治·貝克萊主教在攻擊無窮小量時認為，流數實際上是「消失的量的鬼魂」，是0與0之比。歐拉承認後者，並認為0與0之比可以是有限值。拉格朗日則假定函數都可以展開為冪級數，並在此基礎上定義導數。

十九世紀後，隨着對函數連續性和極限的更深刻認識，微積分終於趨於嚴謹。波爾查諾是首先將導數定義為函數值的改變量與自變量增量之比在自變量增量無限接近0時趨向的量。波爾查諾強調導數不是0與0之比，而是前面的比值趨向的數。柯西在他的著作《無窮小分析教程概論》中也使用了同樣的定義，並定義$dy$ 為導數與 $dx$ 的乘積。這樣，導數和微分的概念得到了統一。

導數的記法

從微積分發軔至如今，不同的數學家都曾使用過不同的記號來表示函數的導數。部分記號至今仍然使用，成為現代的通用記法。

牛頓的記法

作為微積分的發明人之一，牛頓在1704年著作中將導數用函數符號上方的點來表示。例如 $y=f(x)$的導數就記作${\dot {y}}$，而二階導數則記為${\ddot {y}}$。他以後的數學家也會將${\dot {y}}$用來表示函數的微分。牛頓的記法中沒有明確自變量，因此 $y$ 對 $x$ 的導數在牛頓的著作中也會被記成$y':x'$，因為這可以理解為兩個函數$y$ 和 $x$ 對於另一個變量$t$ 的導數比。而這個導數比（使用萊布尼茲的記號）：

$y':x'={\frac {dy}{dt}}:{\frac {dx}{dt}}={\frac {dy}{dx}}$

牛頓的記號多見於物理學或與之有關的方面，如微分方程中。以及直到現在，使用函數符號上加一點來表示某一變量的變化率（即對時間的導數）依然常見於各類物理學教材中（如使用${\dot {v}}$來表示加速度等）。注意到對於高階的導數，這種記法就無法表示了。

萊布尼茲的記法

戈特弗里德·威廉·萊布尼茨

萊布尼茲在他的研究中分別使用 $\Delta x$ 和 $\Delta y$ 來表示函數自變量和應變量（輸出值）的有限變化量，而使用 $dx$ 和 $dy$ 來表示「無限小」的變化量（即所謂的「無窮小量」）。如果將函數記為$y=f(x)$的話，那麼在萊布尼茲的記法下，其導數記為：

${\frac {dy}{dx}}$、${\frac {df}{dx}}(x)$、${\frac {d}{dx}}f(x)$ 或 ${\frac {d\left(f(x)\right)}{dx}},$

這個記法最早出現在萊布尼茲1684年的論文中，萊布尼茲在之前的文章中會將 $dx$ 記成 ${\tfrac {x}{d}}$，把 ${\tfrac {dy}{dx}}$ 記成 $d{\tfrac {y}{x}}$。萊布尼茲記法的好處是明確了自變量和應變量。要注意的是記號$dx$是一個整體，$dy$也是，而${\frac {dy}{dx}}$可以看成一個整體，也可以不嚴謹地看成$dy$和$dx$的比值。此外，${\frac {dy}{dx}}$ 表示的是導函數，在某一點 $x=a$ 的導數則記為：$\left.{\frac {dy}{dx}}\right|_{x=a}$ 對於更高階的導數（比如說n階，見高階導數一節），萊布尼茲的記法是：

${\frac {d^{n}y}{dx^{n}}}$、${\frac {d^{n}f}{dx^{n}}}(x)$ 或 ${\frac {d^{n}\left[f(x)\right]}{dx^{n}}},$

這種記法是在1695年出現的。這裏的分子和分母不再具有單獨的意義。萊布尼茲的記法中使用 ${\frac {d}{dx}}$ 來表示微分算子，比如說二階的導數 ${\frac {d^{2}y}{dx^{2}}}$ 就可以看成：

${\frac {d^{2}y}{dx^{2}}}={\frac {d}{dx}}\left({\frac {dy}{dx}}\right)$

萊布尼茲記法的另一個好處是便於記憶導數計算的法則。例如連鎖律（見導數的計算一節）應用萊布尼茲的記法就是：

${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$

可以想像為右邊是兩個分式的乘積，消去$du$之後就變成左邊。

由於牛頓和萊布尼茲之間關於微積分創始人稱號的持久糾紛，在十八世紀早期的很長時間裏，英國數學界與歐洲大陸的數學界分別採用牛頓和萊布尼茲的記號，涇渭分明。這種情況直到十八世紀後期才開始改變，隨着拉格朗日記法的出現而變得多樣化起來。

拉格朗日的記法

另一種現今常見的記法是十八世紀拉格朗日於1797年率先使用的，以在函數的右上角加上一短撇作為導數的記號。函數 $y=f(x)$ 的導數就記作 $f'(x)$ 或 $y'$。二階和三階導數記為$f''(x)$、$y''$ 和 $f'''(x)$、$y'''$。如果需要處理更高階的導數，則用括號內的求導階數n來代替短撇，記為：$f^{(n)}(x)$、$y^{(n)}$。當十九世紀的數學家柯西處理微分學時，他認為萊布尼茲的記法「模糊不便」，而採用更為「緊湊」的記法，將 ${\frac {dy}{dx}}$ 記為$y'_{x}$。這種記法可說是拉格朗日記法的變種。後來這種記法曾繼續被精簡為$y_{x}$。

其它記法

十九世紀以前，儘管大部分數學家會選擇採用牛頓、萊布尼茲或拉格朗日的記號來表示導數，但也有很多的數學家希望使用自己的方法來記錄。在不同數學家的著作中可以看到各種主流記法的混合或變體。數學家之間關於什麼樣的記法最為簡便和嚴謹也是各執一詞。同時，由於函數的微分、導數、偏導數以及無窮小量等概念尚未成熟，記號的不統一更增加了數學家之間相互理解的難度。十九世紀初期的德國數學家馬爾丹·歐姆採用$\partial f(x)$來表示導數，而同時期的雅可比則採用${\frac {\partial f}{\partial x}}$來表示偏導數。同時許多數學家採用${\frac {df}{dx}}$、${\frac {d}{x}}f$或 ${\frac {\delta f}{\delta x}}$表示偏導數。

用大寫字母$D$表示導數從十八世紀末就開始。1800年，法國數學家路易斯·弗朗索瓦·安托內·阿伯加斯特（Louis François Antoine Arbogast）使用$D^{m}f$表示函數 $f$ 的m階導數或全微分。而其後本傑明·佩爾斯也使用$Df\cdot x$表示 $f$ 對 $x$ 的導數。而柯西也採用類似的記號，用$D_{x}^{m}f$表示函數 $f$ 對 $x$ 的m階偏導數。

函數可導的條件

如果一個函數的定義域為全體實數，即函數在$(-\infty ,+\infty )$上都有定義，那麼該函數是不是在定義域上處處可導呢？答案是否定的。函數在定義域中一點可導需要一定的條件。首先，要使函數$f$在一點可導，那麼函數一定要在這一點處連續。換言之，函數若在某點可導，則必然在該點處連續。這個結論來自於連續性的定義。

證明：

設函數$y=f(x)$上一點$x_{0}$，函數在這一點可導，即$f'(x_{0})=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}$存在，其中

$\Delta y=f(x_{0}+\Delta x)-f(x_{0})$

所以：$\lim _{\Delta x\to 0}\Delta y=\lim _{\Delta x\to 0}\left({\frac {\Delta y}{\Delta x}}\cdot \Delta x\right)=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}\cdot \lim _{\Delta x\to 0}\Delta x=f'(x_{0})\cdot 0=0$ 即函數$f(x)$在$x_{0}$處連續。

符號函數（sgn函數）是一個不連續的函數在斷點處不可導的例子：

符號函數

首先注意到這個函數在$x_{0}=0$處不連續。作為驗證，可以求出函數在$x=0$處附近的變化率，根據函數可導的條件再進行判斷：

該函數在$x_{0}=0$左側附近的變化率為：${\frac {f(x)-f(x_{0})}{x-x_{0}}}={\frac {-1-0}{x-0}}=-{\frac {1}{x}}$

當$x\to 0^{-}$時，上面的比值趨於正無窮大發散，不存在，故這個符號函數在$x_{0}=0$處不可導。

然而，連續性並不能保證可導性。即使函數在一點上連續，也不一定就在這一點可導。事實上，存在着在每一點都連續，但又在每一點都不可導的「病態函數」。1931年，斯特凡·巴拿赫甚至證明，事實上「絕大多數」的連續函數都屬於這種病態函數（至少在一點可導的連續函數在所有連續函數中是貧集）。在連續而不可導的函數裏，一種常見的情況是，函數在某一點連續，並且可以定義它的左導數和右導數：

左導數：$f'_{-}(x_{0})=\lim _{\Delta x\to 0^{-}}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}$ 右導數：$f'_{+}(x_{0})=\lim _{\Delta x\to 0^{+}}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}$

然而左導數和右導數並不相等，因而函數在該處不可導。實際上，若函數導數存在，則必然可以推出左右導數相等，這是由極限的性質（極限存在則左右極限相等）得來：

$\lim _{\Delta x\to 0}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}=\lim _{\Delta x\to 0^{-}}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}=\lim _{\Delta x\to 0^{+}}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}$

下面以絕對值函數作為例子：

絕對值函數

該函數在$x=0$處的左導數為：$f'_{-}(0)=\lim _{x\to 0^{-}}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\to 0^{-}}{\frac {-x-0}{x-0}}=-1$

該函數在$x=0$處的右導數為：$f'_{+}(0)=\lim _{x\to 0^{+}}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\to 0^{+}}{\frac {x-0}{x-0}}=1$

絕對值函數在$x=0$處的左右導數皆存在，但由於左右導數不相等，故絕對值函數在$x=0$處不可導。

如果函數在一點的左右導數都存在並且相等，那麼函數在該處可導。

導數與函數的性質

通過認識可導函數的導數，可以推斷出不少函數本身的性質。

單調性

x變化時函數$\scriptstyle f(x)=1+x\sin(x^{2})$（藍色曲線）的切線變化。函數的導數值就是切線的斜率，綠色代表其值為正，紅色代表其值為負，黑色代表值為零。

根據微積分基本定理，對於可導的函數$f$，有：

$f(b)-f(a)=\int _{a}^{b}f'(t)\mathrm {d} t$

如果函數的導函數在某一區間內恆大於零（或恆小於零），那麼函數在這一區間內單調遞增（或單調遞減），這種區間也稱為函數的單調區間。導函數等於零的點稱為函數的駐點（或極值可疑點），在這類點上函數可能會取得極大值或極小值。進一步判斷則需要知道導函數在附近的符號。對於滿足 $f'(x_{0})=0$ 的一點 $x_{0}$，如果存在 $\delta >0$ 使得 $f'$ 在區間$(x_{0}-\delta ,x_{0}]$ 上都大於等於零，而在區間 $[x_{0},x_{0}+\delta )$ 上都小於等於零，那麼 $x_{0}$ 是一個極大值點，反之則為極小值點。如果$f''(x_{0})=0$ 並且 $f''(x)$ 在 $x_{0}$ 改變加減號，則稱這個點是拐點；否則這個點不是拐點。

如果函數在 $x_{0}$ 處的二階導數 $f''(x_{0})$ 存在，極值點也可以用它的正負性判斷（已確定$f'(x_{0})=0$）。如果$f''(x_{0})>0$，那麼 $x_{0}$ 是一個極小值點，反之為極大值點。

凹凸性

主條目：凸函數和凹函數

可導函數的凹凸性與其導數的單調性有關。如果函數的導函數在某個區間上單調遞增，那麼這個區間上函數是向下凸的，反之則是向上凸的。如果二階導函數存在，也可以用它的正負性判斷，如果在某個區間上 $f''$ 恆大於零，則這個區間上函數是向下凸的，反之這個區間上函數是向上凸的。

導數的計算

原則上，函數的導數可以通過考慮差商和計算其極限來從定義計算。在實踐中，一旦知道了一些簡單函數的導數，就可以使用從更簡單的函數獲得更複雜函數的導數的規則，來更容易地計算其他函數的導數。

基本函數的導數

主條目：導數列表

所謂基本函數是指一些形式簡單並且容易求出導數的函數。這些基本函數的導函數可以通過定義直接求出。

• 冪函數的導數：如果

$f(x)=x^{r},$

其中$r$是任意實數，那麼

$f'(x)=rx^{r-1},$函數$f$的定義域可以是整個實數域，但導函數的定義域則不一定與之相同。例如當 $r={\frac {1}{2}}$時：

$f'(x)={\frac {1}{2}}x^{-{\tfrac {1}{2}}}\,$

導函數的定義域只限所有正實數而不包括0。需要注意的是，不會有多項式函數的導數為$\scriptstyle x^{-1}$。當 $r=0$ 時，常函數的導數是0。

• 底數為$e$的指數函數 $\scriptstyle y=e^{x}$ 的導數還是自身：$\scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}.$ 而一般的指數函數 $y=a^{x}$ 的導數還需要乘以一個系數：$\scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}a^{x}=\ln(a)a^{x}.$

自然對數函數的導數則是 $x^{-1}$：$\scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}\ln(x)={\frac {1}{x}},\qquad x>0.$ 同樣的，一般的對數函數導數則還需要乘以一個系數：$\scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}\log _{a}(x)={\frac {1}{x\ln(a)}}$

• 三角函數的導數仍然是三角函數，或者由三角函數構成:

${\frac {d}{dx}}\sin(x)=\cos(x).$

${\frac {d}{dx}}\cos(x)=-\sin(x).$

${\frac {d}{dx}}\tan(x)=\sec ^{2}(x)={\frac {1}{\cos ^{2}(x)}}=1+\tan ^{2}(x).$

${\frac {\mathrm {d} }{\mathrm {d} x}}\cot(x)=-\csc ^{2}(x)=-{\frac {1}{\sin ^{2}(x)}}.$

• 反三角函數的導數則是無理分式:

${\frac {d}{dx}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1.$

${\frac {d}{dx}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1.$

${\frac {d}{dx}}\arctan(x)={\frac {1}{1+x^{2}}}$

導數的求導法則

主條目：求導法則

由基本函數的和、差、積、商或相互複合構成的函數的導函數則可以通過函數的求導法則來推導。基本的求導法則如下：

• 求導的線性性：對函數的線性組合求導，等於先對其中每個部分求導後再取線性組合。

$(af+bg)'=af'+bg'\,$ （其中$a,b$為常數）

• 兩個函數的乘積的導函數，等於其中一個的導函數乘以另一者，加上另一者的導函數與其的乘積

$(fg)'=f'g+fg'\,$

• 兩個函數的商的導函數也是一個分式。其中分子是分子函數的導函數乘以分母函數減去分母函數的導函數乘以分子函數後的差，而其分母是分母函數的平方。

$\left({\frac {f}{g}}\right)'={\frac {f'g-fg'}{g^{2}}}$ （在$g(x)\neq 0$處方有意義）

• 複合函數的求導法則：如果有複合函數 $f(x)=h[g(x)]$，那麼

$f'(x)=h'[g(x)]\cdot g'(x).\,$

若要求某個函數在某一點的導數，可以先運用以上方法求出這個函數的導函數，再看導函數在這一點的值。

例子

欲求函數

$f(x)=x^{4}+\sin(x^{2})-\ln(x)e^{x}+7\,$

在$x=3$處的導數。可以先求出其導函數：

${\begin{aligned}f'(x)&=4x^{(4-1)}+{\frac {\mathrm {d} \left(x^{2}\right)}{\mathrm {d} x}}\cos(x^{2})-\left[{\frac {\mathrm {d} \left(\ln {x}\right)}{\mathrm {d} x}}e^{x}+\ln {x}{\frac {\mathrm {d} \left(e^{x}\right)}{\mathrm {d} x}}\right]+0\\&=4x^{3}+2x\cos(x^{2})-{\frac {1}{x}}e^{x}-\ln(x)e^{x}.\end{aligned}}$

其中第二項使用了複合函數的求導法則，而第三項則使用了乘積的求導法則。求出導函數後，再將$x=3$代入，得到導數為：

$f'(3)=108+6\cos(9)-{\frac {e^{3}}{3}}-\ln(3)e^{3}\,$

高階導數

二階導數

主條目：二階導數

如果函數的導數$f'(x)\,$在$x\,$處可導，則稱$[f'(x)]'\,$為$x\,$的二階導數。記做：$f''(x)\,$，$y''\,$，${\frac {{\rm {d}}^{2}y}{{\rm {d}}x^{2}}}$或${\frac {{\rm {d}}^{2}f(x)}{{\rm {d}}x^{2}}}$、

二階導數可用於求解函數凹凸性問題。 $f''(x)>0$函數在x上凹。 $f''(x)<0$函數在x下凹。

高階導數

二階導數的導數稱為三階導數，記做$f'''(x)\,$，$y'''\,$，${\frac {{\rm {d}}^{3}y}{{\rm {d}}x^{3}}}$或${\frac {{\rm {d}}^{3}f(x)}{{\rm {d}}x^{3}}}$

三階導數的導數稱為四階導數，記做$f^{(4)}(x)\,$，$y^{(4)}\,$，${\frac {{\rm {d}}^{4}y}{{\rm {d}}x^{4}}}$或${\frac {{\rm {d}}^{4}f(x)}{{\rm {d}}x^{4}}}$

一般的$f(x)\,$的$n-1\,$階導數的導數稱為$f(x)\,$的$n\,$階導數，記為$f^{(n)}(x)\,$，$y^{(n)}\,$，${\frac {{\rm {d}}^{n}y}{{\rm {d}}x^{n}}}$或${\frac {{\rm {d}}^{n}f(x)}{{\rm {d}}x^{n}}}$

高階導數的求法

一般來說，高階導數的計算和導數一樣，可以按照定義逐步求出。同時，高階導數也有求導法則：

• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}(u\pm v)={\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}u\pm {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}v$
• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}(Cu)=C{\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}u\$
• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}(u\cdot v)=\sum _{k=0}^{n}C_{k}^{n}{\frac {{\rm {d}}^{n-k}}{{\rm {d}}x^{n-k}}}u{\frac {{\rm {d}}^{k}}{{\rm {d}}x^{k}}}v$（萊布尼茲公式）

因此，可以利用已知的高階導數求導法則，通過四則運算, 變量代換等方法，求出$n\$階導數。一些常見的有規律的高階導數的公式如下：

• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}x^{\alpha }=x^{\alpha -n}\prod _{k=0}^{n-1}(\alpha -k)$
• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}{\frac {1}{x}}=(-1)^{n}{\frac {n!}{x^{n+1}}}$
• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\ln x=(-1)^{n-1}{\frac {(n-1)!}{x^{n}}}$

$\!$

• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}e^{x}=e^{x}\$
• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}a^{x}=a^{x}\cdot \ln ^{n}a$ $(a>0)\$

$\!$

• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\sin \left(kx+b\right)=k^{n}\sin \left(kx+b+{\frac {n\pi }{2}}\right)$
• ${\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\cos \left(kx+b\right)=k^{n}\cos \left(kx+b+{\frac {n\pi }{2}}\right)$

多元函數的導數

主條目：向量分析

向量值函數的導數

當函數 $y$ 的取值不再是實數，而是一般的$\mathbf {R} ^{n}$中的向量時，仍然可能對其求導。這時的函數值是：$y=\left(y_{1}(x),y_{2}(x),\cdots ,y_{n}(x)\right)$。每個 $y_{i}(x),\;\;1\leqslant i\leqslant n$ 都是一個實數值的函數。具體的例子如二維或者三維空間裏的參數方程。因此，對 $y=f(x)$ 求導實際上是對每個分量函數 $y_{i}(x)$ 求導。

$\mathbf {y} '(t)=(y'_{1}(t),\cdots ,y'_{n}(t)).$

這也符合定義

$\mathbf {y} '(t)=\lim _{h\to 0}{\frac {\mathbf {y} (t+h)-\mathbf {y} (t)}{h}},$

設$\left(e_{1},e_{2},\cdots e_{n}\right)$為$\mathbf {R} ^{n}$的一組基，那麼對函數：$y\,:t\,\mapsto \,y_{1}(t)e_{1}+y_{2}(t)e_{2}+\cdots y_{n}(t)e_{n},$

其導函數為：$y'(t)=y'_{1}(t)e_{1}+y'_{2}(t)e_{2}+\cdots y'_{n}(t)e_{n}$

偏導數

主條目：偏導數

如果有函數 $f$ 其自變量不是單個實數，而是多於一個元素，例如：

$f(x,y)=x^{2}+xy+y^{2}.\,$

這時可以把其中一個元素（比如 $x$ ）看做參數，那麼 $f$ 可以看做是關於另一個元素的參數函數：

$f(x,y)=f_{x}(y)=x^{2}+xy+y^{2}.\,$

也就是說，對於某個確定的 $x$，函數 $f_{x}$ 就是一個關於 $y$ 的函數。在 $x=a$ 固定的情況下，可以計算這個函數 $f_{x}$ 關於 $y$ 的導數。

$f_{a}'(y)=a+2y\,$

這個表達式對於所有的 $a$ 都對。這種導數稱為偏導數，一般記作：

${\frac {\partial f}{\partial y}}(x,y)=x+2y$

這裏的符號 ∂ 是字母 $d$ 的圓體變體，一般讀作 $\delta$ 的首音節或讀「偏」，以便與 $d$ 區別。

更一般地來說，一個多元函數 $f\left(x_{1},x_{2},\cdots ,x_{n}\right)$ 在點 $\left(a_{1},a_{2},\cdots ,a_{n}\right)$ 處對 $x_{i}$ 的偏導數定義為：

${\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n})=\lim _{h\to 0}{\frac {f(a_{1},\ldots ,a_{i}+h,\ldots ,a_{n})-f(a_{1},\ldots ,a_{n})}{h}}.$

上面的極限中，除了 $x_{i}$ 外所有的自變元都是固定的，這就確定了一個一元函數：

$f_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}(x_{i})=f(a_{1},\ldots ,a_{i-1},x_{i},a_{i+1},\ldots ,a_{n})$

因此，按定義有：

${\frac {df_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}}{dx_{i}}}(a_{i})={\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n}).$

偏導數的實質仍然是一元函數的導數。

多變量函數的一個重要的例子，是從$\mathbf {R} ^{n}$（例如 $\mathbf {R} ^{2}$ 或 $\mathbf {R} ^{3}$）映射到$\mathbf {R}$上的純量值函數 $f\left(x_{1},x_{2},\cdots ,x_{n}\right)$。在這種情況下，$f$ 關於每一個變量 $x_{i}$ 都有偏導數${\frac {\partial f}{\partial x_{i}}}$。在點 $x={\boldsymbol {a}}$，這些偏導數定義了一個向量：

$\nabla f({\boldsymbol {a}})=\left[{\frac {\partial f}{\partial x_{1}}}({\boldsymbol {a}}),\ldots ,{\frac {\partial f}{\partial x_{n}}}({\boldsymbol {a}})\right]$。

這個向量稱為 $f$ 在點 ${\boldsymbol {a}}$ 的梯度。如果 $f$ 在定義域中的每一個點都是可微的，那麼梯度便是一個向量值函數 $\nabla f$，它把點 $a$ 映射到向量 $\nabla f(a)$。這樣，梯度便決定了一個向量場。

方向導數

主條目：方向導數

方向導數是比偏導數更加廣泛的概念。導數的本質是函數值增量與自變量增量之比的極限。在多元函數 $f$ 中，可以選定一個確定的方向（以這個方向上的單位向量 ${\boldsymbol {\delta }}$ 表示），並考慮函數在這個方向上的增量：

$f({\boldsymbol {x}}_{0}+t{\boldsymbol {\delta }})-f({\boldsymbol {x}}_{0})$

這個增量為關於 $t$ 的一元函數。函數 $f$ 的方向導數定義為這個增量與 $t$ 的比值在 $t$ 趨於0時的極限，記為${\frac {\partial f}{\partial {\boldsymbol {\delta }}}}({\boldsymbol {x}}_{0})$。

${\frac {\partial f}{\partial {\boldsymbol {\delta }}}}({\boldsymbol {x}}_{0})=\lim _{t\to 0}{\frac {f({\boldsymbol {x}}_{0}+t{\boldsymbol {\delta }})-f({\boldsymbol {x}}_{0})}{t}}$

方向導數表示了函數從某點開始在某個方向上的變化率。

在$\mathbf {R} ^{n}$中，如果將向量 ${\boldsymbol {\delta }}$ 選為正規基 $\left({\boldsymbol {e}}_{1},{\boldsymbol {e}}_{2},\cdots ,{\boldsymbol {e}}_{n}\right)$ 之中的一個，如${\boldsymbol {e}}_{i}$，那麼方向導數就是關於 ${\boldsymbol {x}}_{i}$ 的偏導數。

推廣

導數的概念建立在變量為實數之上，但也可以推廣到更加廣泛的意義上。推廣的導數本質上仍舊是函數在局部一點上的線性逼近。

復變量導數

主條目：全純函數

對於變量為複數的函數，也可以定義導數的概念。假設有複變函數$f:\Omega \in \mathbb {C} \to \mathbb {C}$。如果 $f$ 在某一點 $z_{0}$ 及附近有定義，並且極限：

$\lim _{z\to z_{0}}{\frac {f(z)-f(z_{0})}{z-z_{0}}}$

存在，那麼就說函數 $f$ 在 $z_{0}$ 可導。其中 $z\to z_{0}$ 表示 $z-z_{0}$ 的模長趨向於0。如果將復變量 $z$ 視作 $x+iy$，那麼 $f$ 可以視作一個$\mathbb {R} ^{2}$上的函數。如果作為複變函數的 $f$ 可導，那麼作為$\mathbb {R} ^{2}$上函數的 $f$ 的偏導數也存在，但反之則不然。只有當柯西-黎曼條件滿足的時候才能保證複變函數的復可導性。

弱微分

主條目：弱微分

在分佈理論里，弱微分的概念使得對更多嚴格意義上無法求導的函數也可以定義導函數。設$u$是一個局部勒貝格可積（比如說在$L_{loc}^{1}(\mathbb {R} )\$中）的函數，稱$v\in L_{loc}^{1}(\mathbb {R} )$是$u$的一個弱微分，如果對所有的測試函數$\varphi$，都有：

$\int _{\mathbb {R} }u(t)\varphi '(t)dt=-\int _{\mathbb {R} }v(t)\varphi (t)dt$

成立。其中測試函數是指緊支撐的光滑函數。弱微分包括了強微分，也就是通常意義上的導數。

次導數

主條目：次導數

過$x_{0}$的直線（紅）在函數（藍）下方，它的斜率是函數的次導數

在凸分析，也就是對凸函數的研究中，可以定義凸函數的次導數。次導數的概念是導數的幾何意義的推廣。由於函數是凸的，過它的圖像上每一點總可以作一條直線，使得函數的圖像在直線上方。這種直線的斜率稱為函數在這點的次導數。如果函數在某點可導，那麼次導數只有一個，等於其導數。如果函數像絕對值函數一樣在零點有突然的轉折，那麼次導數可能不止一個。比如過零點而斜率在$(-1,1)$之間的直線都在絕對值函數下方，因此$(-1,1)$之間的每個數都是絕對值函數在零點的次導數。

非整數階導數

主條目：分數微積分

早在十九世紀，在數學家明確了求導與積分的互逆關係以後，就出現了負階次導數的記號：$D^{-n}=\int ^{n}$（表示求n次積分）。而非整數階導數的概念則進一步將其推廣。比如，半微分算子$H=D^{\frac {1}{2}}$表示其作用於函數上兩次以後的效果將等於一次求導：

$H^{2}(f)(x)=H[H(f)](x)=D(f)(x)=f'(x)$

定義非整數階導數的方法不止一種，最常用的非整數階導數定義為黎曼-萊歐維爾定義：

設$0<s<1$，函數 $f$ 的s階積分為：$D_{t}^{-s}f(t)={\frac {1}{\Gamma (s)}}\int _{a}^{t}(t-u)^{s-1}f(u)d(u)$

而對$n-1<\beta <n$，函數 $f$ 的$\beta$階導數為：$D_{t}^{\beta }f(t)={\frac {d^{n}}{dt^{n}}}\left[D_{t}^{-n-\beta }f(t)\right]$

加托導數和弗雷歇導數

方向導數在無窮維向量空間如巴拿赫空間和弗雷歇空間上可以推廣為加托導數和弗雷歇導數。二者都經常用於形式化泛函導數的概念，常見於物理學，特別是量子場論。

導子

主條目：導子

微分代數中有導子的概念。導子是具備了微分算子的某些特徵的運算子，例如向量場的李導數，或非交換代數中的交換子。給定一個環或域 $\mathbf {R}$ 上的一個代數 ${\mathcal {A}}$，${\mathcal {A}}$ 上的一個$\mathbf {R}$-導子 $\delta$ 是一個從 ${\mathcal {A}}$ 射到自身的$\mathbf {R}$-線性映射（線性自同態），並滿足導數的乘積法則：

$\delta (ab)=(\delta a)b+a(\delta b)$

所有$\mathbf {R}$-導子構成了 ${\mathcal {A}}$ 上線性自同態集 $\operatorname {End} {\mathcal {A}}$ 的子空間。

導數的應用

物理學、幾何學、工程科學、經濟學等學科中的一些重要概念都可以用導數來表示。如，導數可以表示運動物體的瞬時速度和加速度，也可以表示曲線在一點的斜率。

邊際和彈性

經濟學中，所謂邊際和彈性的概念與導數緊密相關。比如邊際成本就是產量增加一個單位所帶來的成本的增加，若將其連續化，得到的便是成本函數的導數。又如需求的彈性是指價格變化一個單位時，需求量的變化，連續化後相應的也是需求函數關於價格的導數。

參見

• 導數列表
• 微積分
• 微分
• 積分
• 光滑函數
• 微分中值定理
• 介值定理
• 自動微分
• 第二次數學危機
• 協變導數
• 數值微分

外部連結

• 導數計算器 （頁面存檔備份，存於互聯網檔案館）
• Hazewinkel, Michiel (編), Derivative, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 
• 埃里克·韋斯坦因. Derivative. MathWorld.