光学

光学(英语:Optics),是物理学的分支领域,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射例如X射线、微波及无线电波等等也具有类似光的特性。[1]英文术语“optics”源自古希腊字“ὀπτική”,意为名词“看见”、“视见”。[2]
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。它试图将光当作射线(光线),能够直线移动,并且在遇到不同介质时会改变方向;它能够解释像直线传播、反射、折射等等很多光线现象。物理光学的模型比较精密,它把光当作是传播于介质的波动(光波)。除了反射、折射以外,它还能够以波性质来解释向前传播、干涉、偏振等等光学现象。几何光学不能解释这些比较复杂的光学现象。在历史上,光的射线模形首先被发展完善,然后才是光的波动模形.
很多现象涉及到光的波粒二象性。只有量子力学能够解释这些现象。在量子力学里,光被视为由一群称为光子的粒子组成。量子光学专门研究怎样用量子力学来解释光学现象。
进一步将光学细分类。光的纯科学领域,通常被称为光学或“光学物理”。应用光学通常被称为光学工程。光学工程中涉及到照明系统的部分,被特别称为“照明工程”。每一个分支在应用、技术、焦点以及专业关联上,都有很大不同。在光学工程中,比较新的发现,通常被归类为光子学(photonics)。
因为光学在实际中被广泛应用,光学物理和工程光学,在领域上,有很大程度的互相交叉。光学也与电子工程、物理学、天文学、医学(尤其是眼科学与视光学)等许多学科密切相关。很多关键科技都能找到光学的研究果实,包括镜子、透镜、望远镜、显微镜、镭射、光纤、发光二极管、光伏等等。
经典光学
[编辑]在量子光学的重要性被揭示之前,光学的基本理论主要是经典电磁场理论以及它在光学领域的高频近似。经典光学可以分成两个主要分支:几何光学与物理光学。
几何光学
[编辑]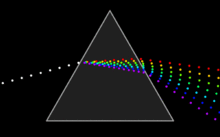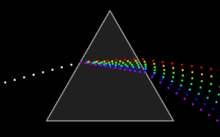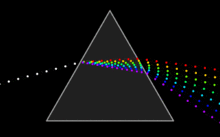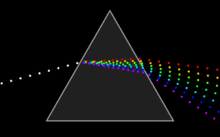
几何光学,又称射线光学,描述了光的传播。在几何光学中,光被称作是 "射线"(光线)。光线会在两种不同介质的界面改变传播方向,并有可能在折射率随位置变化的介质中发生曲线弯折的现象。几何光学中的“光线”是抽象的物体,它的前进方向垂直于光波的波前。几何光学给出了光线通过光学系统的传播规律,以此可以预测其实际波前的位置。费马原理是几何光学的基本定理:光传播的路径是光以最短时间通过的路径[3],由此可以推导出许多几何光学的定律。考虑一个由透镜、反射镜及棱镜组合而成的光学系统,用几何光学可以说明其中的反射、折射等现象,需要注意的是,几何光学简化了光学理论,因此它无法解释很多重要的光学效应,例如:衍射、偏振等。
通过近轴近似(也称为小角近似),可以对几何光学做进一步简化,并对应于数学描述上的线性化。在近轴近似条件下,光学元件和系统可以通过简单的矩阵来表示。高斯光学以及近轴光线跟踪都是以近轴近似的基础进行发展,可以确定光学系统的一阶特性,例如找出成像位置、物体位置以及放大倍率的近似值等[4]。高斯光束传播是近轴光学的扩展,它可以更为精确地描述相干传播(如镭射光束)。即使仍然使用近轴近似,这一技术可以部分描述衍射,能够精确计算镭射束随距离传播的速率以及其最小的汇聚尺寸。高斯光束传播理论因此可以沟通几何光学与物理光学。
物理光学
[编辑]物理光学,或称波动光学,建立在惠更斯原理之上,可以建立复波前(包括振幅与相位)通过光学系统的模型。这一技术能够利用计算机数值仿真模拟或计算衍射、干涉、散射、偏振特性、像差等各种复杂光学现象。物理光学名称中的“物理”表示它比几何光学更接近物理原理,但仍然只是物理理论的近似而已[5]:11-13。由于仍然有所近似,因此物理光学不能像电磁波理论模型那样能够全面描述光传播。对于大多数实际问题来说,完整电磁波理论模型计算量太大,在现在的一般计算机硬件条件下并不十分实用,但小尺度的问题可以使用完整波动模型进行计算。
近代光学
[编辑]近代光学包括了二十世纪开始研究的光学科学及光学工程。光学科学部分一般会和光的电磁特性或是量子特性(光子)有关,不过也包括其他领域。量子光学是近代光学的主要子领域之一,处理光的量子力学特性。量子光学不只是理论而已,像镭射等现代光学设备其中的原理都是以量子光学为基础。像光电倍增管或电子倍增管等光侦测器可以对单一光子反应。像感光耦合元件等电子式的图像传感器,也会因为个别光子的统计特性而出现散粒噪声。若没有量子力学,也就无法理解发光二极管及太阳能电池的原理。量子光学常和量子电子学重叠[6]。
特别领域的光学研究也包括光和特定材料之间的关系(如晶体光学及超材料),其他的研究包括电磁波的现象,以及光学涡旋、非成像光学、非线性光学、统计光学、光度学及辐射度量学等。此外,电脑工程师对积体光学、机器视觉及光学计算等有兴趣,这些可能是下一代电脑中的重要组件[7]。
现在,光学中纯物理的部分会称为光物理学,和光学中应用科学或工程的部分分开,后者则称为光电工程。光电工程的主要领域包括有照明工程、光子学及光电工程等,实务应用光学透镜设计、光学构件的制作和检测及影像处理等。其中部分领域有些重叠,而各概念的差异在不同的地区或是不同的产业也会略有不同。因为镭射技术的进展,在数十年前就开始了一个非线性光学的专业研究社群[8]。
光学的应用
[编辑]每天生活中有许多都和光学有关。生物的视觉系统就是以光学原理运作,是五感之一。眼镜或隐形眼镜帮助人们改善视力,而光学也是许多消费性产品(例如相机)的重要机能,望远镜、显微镜及放大镜都是典型的光学仪器。彩虹及海市蜃楼都是光学现象,而光通讯是现在互联网及电话学的基础。
人眼
[编辑]
人眼的功能是将光线聚焦在称为视网膜,位在眼球内部后方的感光细胞。聚焦是由一系列的透光物质来达成。进入眼球的光会先通过角膜,之后通过角膜后的液态区域眼球前房,接着进入瞳孔。光之后通过可以调节及聚焦光线的晶状体,接着会经过人眼中的主要液态区域玻璃体,最后进入视网膜。视网膜的细胞在眼球内侧的后面,只有一点是视神经离开眼球的路径,这个点也是眼睛的盲点。
眼睛中有两种感光细胞,分别是视杆细胞及视锥细胞,会以不同的方式感测光线[9]。视杆细胞对广泛频率范围内的光强度变化很敏感,负责黑白视觉,视杆细胞分布在正中凹的区域,对于光在空间中的变化或是随时间的变化不如视锥细胞那么敏感。不过视杆细胞在视网膜中分布的区域较广,且数量是视锥细胞的二十倍,因为其分布位置的广泛,视杆细胞负责外围视觉[10]。
视锥细胞对光的整体强度变化较不敏感,但视锥细胞分为三种,对三个不同频率范围的光很敏感,因此用来认知颜色及亮视觉。视锥细胞集中在正中凹,其空间的分辨率较视杆细胞要好。因为视锥细胞在光线暗时不像视杆细胞那么灵敏,夜间视觉会因为而受限。因为视锥细胞集中在正中凹,大部分的中央视觉(例如阅读、做精细动作或检查物品需要的视觉)都是由视锥细胞进行[10]。
大气光学
[编辑]
大气独特的光学特性造成很多壮观的光学现象,像天空的蓝色就是瑞利散射的结果,将较高频率的颜色(蓝色)反射到观察者眼前。因为蓝光比红光容易被散射,当透过较厚的太气来直接观测太阳(如日出或日落)时,太阳会呈现红色。天空中其他颗粒物也可以在不同角度散射不同颜色的光,因此在黄昏和黎明时会有多彩发光的天空。大气中冰晶或其他物质的散射造成了晕、晚霞余晖、华、云隙光及幻日等大气现象。这些现象的不同是因为空气中粒子的大小及其几何形状[11]。
海市蜃楼是光因为不同温度下空气折射率的变化而产生的光学现象。光线在传播于不同温度下的空气时被偏折而在遥远的距离或天空中生成虚像,因此物体会出现于原先不可能出现的位置。其他相关的光学效应包括新地岛效应,也就是太阳上升的比预期时间要快,而且形状扭曲。复杂蜃景是和逆温下的折射有关的光学现象,是像岛屿、悬崖、船舶及冰山等物体在地平线上,其外形伸长且拉高,看起来像“童话故事里的城堡”[12]。
彩虹是光在雨滴中的内反射及色散折射所造成。若在雨滴中只有单一反射,会在天空仰角约40°至42°度形成彩虹,红色在最外层,若是在雨滴中有二次反射,会在天空仰角约50.5°至54°形成彩虹,紫色在最外层。因为太阳和彩虹的中心会相差180度,若太阳越靠近地平线,彩虹会更明显[13]。
相关条目
[编辑]- 经典光学
- 近代光学
- 光学建模与仿真方法
- 统计光学
- 应用
- 照明工程
- 光学显示
参考资料
[编辑]- ^ McGraw-Hill Encyclopedia of Science and Technology 5th. McGraw-Hill. 1993.
- ^ Online Etymology Dictionary. [2012-07-05]. (原始内容存档于2012-08-21).
- ^ Arthur Schuster An Introduction to the Theory of Optics, London: Edward Arnold, 1904 online (页面存档备份,存于互联网档案馆).
- ^ Greivenkamp, John E. Field Guide to Geometrical Optics. SPIE Field Guides 1. SPIE. 2004: 19–20. ISBN 0-8194-5294-7.
- ^ Pyotr Ya. Ufimtsev. Fundamentals of the Physical Theory of Diffraction. John Wiley & Sons. 9 February 2007. ISBN 978-0-470-10900-7.
- ^ D. F. Walls and G. J. Milburn Quantum Optics (Springer 1994)
- ^ Alastair D. McAulay. Optical computer architectures: the application of optical concepts to next generation computers. Wiley. 16 January 1991 [12 July 2012]. ISBN 978-0-471-63242-9. (原始内容存档于2016-04-25).
- ^ Y. R. Shen. The principles of nonlinear optics. New York, Wiley-Interscience. 1984. ISBN 0-471-88998-9.
- ^ D. Atchison and G. Smith. Optics of the Human Eye. Elsevier. 2000. ISBN 0-7506-3775-7.
- ^ 10.0 10.1 E. R. Kandel, J. H. Schwartz, T. M. Jessell. Principles of Neural Science 4th. New York: McGraw-Hill. 2000: 507–513. ISBN 0-8385-7701-6.
- ^ C. D. Ahrens. Meteorology Today: an introduction to weather, climate, and the environment 5th. West Publishing Company. 1994: 88–89. ISBN 0-314-02779-3.
- ^ A. Young. An Introduction to Mirages. [2015-09-19]. (原始内容存档于2000-10-10).
- ^ H. D. Young. University Physics 8e. Addison-Wesley. 1992. ISBN 0-201-52981-5.Chapter 34
- Hecht, Eugene. Optics (4th ed.). Pearson Education. 2001. ISBN 978-0-8053-8566-3.
- Serway, Raymond A.; Jewett, John W. Physics for Scientists and Engineers (6th ed.). Brooks/Cole. 2004. ISBN 978-0-534-40842-8.
- Tipler, Paul. Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. 2004. ISBN 978-0-7167-0810-0.
教科书
[编辑]- Optics(页面存档备份,存于互联网档案馆) — an open-source Optics textbook
- Optics2001(页面存档备份,存于互联网档案馆) — Optics library and community
