旋轉平面
| 几何学 |
|---|
 |
| 几何学家 |
|
|
旋轉面、旋轉平面(英語:plane of rotation),是一個用於描述空間旋轉的抽像概念。
十維以下的旋轉平面數量如下表所示:
維數 零 一 二 三 四 五 六 七 八 九 十 旋轉平面 0 0 1 1 2 2 3 3 4 4 5
旋轉平面主要用作描述四維空間及以上的旋轉,將高維旋轉分解為簡單的幾何代數描述。 [1]
數學上,旋轉平面可用多種方式描述。可用平面和旋轉角度來描述,可用克利福德代數的二重向量來描述。旋轉平面又與旋轉矩陣的特徵值和特徵向量有關。
In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.
旋轉平面在二維和三維中使用不多,因為在二維中只有一個平面(因此,識別旋轉平面是微不足道的並且很少這樣做),而在三維中旋轉軸具有相同的目的,並且是更成熟的方法。
Planes of rotation are not used much in two and 三維空間s, as in two dimensions there is only one plane (so, identifying the plane of rotation is trivial and rarely done), while in three dimensions the axis of rotation serves the same purpose and is the more established approach. The main use for them is in describing more complex rotations in higher dimensions, where they can be used to break down the rotations into simpler parts. This can be done using geometric algebra, with the planes of rotations associated with simple bivectors in the algebra.[1]
定義
[编辑]平面
[编辑]For this article, all planes are planes through the origin, that is they contain the zero vector. Such a plane in <span class="ilh-all " data-orig-title="'"`UNIQ--templatestyles-00000015-QINU`"'n-dimensional space" data-lang-code="en" data-lang-name="英语" data-foreign-title="n-dimensional space">[[:n-dimensional space|n-dimensional space]] is a two-dimensional linear subspace of the space. It is completely specified by any two non-zero and non-parallel vectors that lie in the plane, that is by any two vectors a and b, such that
where ∧ is the exterior product from exterior algebra or geometric algebra (in three dimensions the cross product can be used). More precisely, the quantity a ∧ b is the bivector associated with the plane specified by a and b, and has magnitude |a| |b| sin φ, where φ is the angle between the vectors; hence the requirement that the vectors be nonzero and nonparallel.[2]
If the bivector a ∧ b is written B, then the condition that a point lies on the plane associated with B is simply[3]
This is true in all dimensions, and can be taken as the definition on the plane. In particular, from the properties of the exterior product it is satisfied by both a and b, and so by any vector of the form
with λ and μ real numbers. As λ and μ range over all real numbers, c ranges over the whole plane, so this can be taken as another definition of the plane.
旋轉平面
[编辑]A plane of rotation for a particular rotation is a plane that is mapped to itself by the rotation. The plane is not fixed, but all vectors in the plane are mapped to other vectors in the same plane by the rotation. This transformation of the plane to itself is always a rotation about the origin, through an angle which is the angle of rotation for the plane.
Every rotation except for the identity rotation (with matrix the identity matrix) has at least one plane of rotation, and up to
planes of rotation, where n is the dimension.
十維以下的旋轉平面數量如下表所示:
維數 零 一 二 三 四 五 六 七 八 九 十 旋轉平面 0 0 1 1 2 2 3 3 4 4 5
When a rotation has multiple planes of rotation they are always orthogonal to each other, with only the origin in common. This is a stronger condition than to say the planes are at right angles; it instead means that the planes have no nonzero vectors in common, and that every vector in one plane is orthogonal to every vector in the other plane. This can only happen in four or more dimensions. In two dimensions there is only one plane, while in three dimensions all planes have at least one nonzero vector in common, along their line of intersection.[4]
In more than three dimensions planes of rotation are not always unique. For example the negative of the identity matrix in four dimensions (the central inversion),
describes a rotation in four dimensions in which every plane through the origin is a plane of rotation through an angle π, so any pair of orthogonal planes generates the rotation. But for a general rotation it is at least theoretically possible to identify a unique set of orthogonal planes, in each of which points are rotated through an angle, so the set of planes and angles fully characterise the rotation.[5]
二維
[编辑]在二維空間只有一個旋轉平面,即空間本身的平面。在笛卡爾坐標系是笛卡爾平面,在複數是複平面。因此,任何旋轉都是整個平面空間的旋轉,僅原點保持固定。完全由帶符號的旋轉角度指定,例如在 -π 到 π 的範圍內。因此若角度為θ,復平面的旋轉則由以下歐拉公式給出:
三維
[编辑]

三維空間可以有無數個旋轉平面,但當旋轉平面有了一個,就不能第二個旋轉平面。
三維任何旋轉都總是只有一個固定的軸,即旋轉軸。
這可以用如下矩陣來描述(旋轉角度為θ):
另一例子是地球自轉。自轉軸是北極至南極的連線,自轉平面穿過北半球和南半球之間的赤道平面。
其它例子包括陀螺儀、飛輪等機械裝置,通常沿旋轉平面儲存大量旋轉動能。
In three-dimensional space there are an infinite number of planes of rotation, only one of which is involved in any given rotation. That is, for a general rotation there is precisely one plane which is associated with it or which the rotation takes place in. The only exception is the trivial rotation, corresponding to the identity matrix, in which no rotation takes place.
In any rotation in three dimensions there is always a fixed axis, the axis of rotation. The rotation can be described by giving this axis, with the angle through which the rotation turns about it; this is the axis angle representation of a rotation. The plane of rotation is the plane orthogonal to this axis, so the axis is a surface normal of the plane. The rotation then rotates this plane through the same angle as it rotates around the axis, that is everything in the plane rotates by the same angle about the origin.
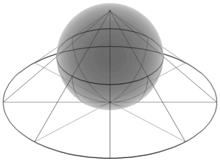
One example is shown in the diagram, where the rotation takes place about the z-axis. The plane of rotation is the xy-plane, so everything in that plane it kept in the plane by the rotation. This could be described by a matrix like the following, with the rotation being through an angle θ (about the axis or in the plane):

Another example is the 地球自转. The axis of rotation is the line joining the North Pole and 南极 and the plane of rotation is the plane through the equator between the Northern and Southern Hemispheres. Other examples include mechanical devices like a gyroscope or flywheel which store rotational energy in mass usually along the plane of rotation.
在任何三維旋轉中,旋轉平面都是唯一定義的。它與旋轉角度一起完整地描述了旋轉。或者,在連續旋轉的物體中,旋轉特性(例如旋轉速率)可以用旋轉平面來描述。
In any three dimensional rotation the plane of rotation is uniquely defined. Together with the angle of rotation it fully describes the rotation. Or in a continuously rotating object the rotational properties such as the rate of rotation can be described in terms of the plane of rotation. It is perpendicular to, and so is defined by and defines, an axis of rotation, so any description of a rotation in terms of a plane of rotation can be described in terms of an axis of rotation, and vice versa. But unlike the axis of rotation the plane generalises into other, in particular higher, dimensions.[7]
四維
[编辑]一般四維旋轉只有一個固定點,即原點。因此,四個維度沒有旋轉軸。但是四維空間可以使用旋轉平面,並且在四個維度中的每個非平凡旋轉都可以有一至兩個旋轉平面。
簡單旋轉
[编辑]僅具有一個旋轉平面的旋轉是簡單旋轉。
簡單旋轉有一個固定的平面,因此點在旋轉時不會改變其與該平面的距離。旋轉平面與該平面正交,可以說旋轉發生在該平面內。
例如,下列矩陣固定 xy 平面:此平面中的點且僅在該平面中的點保持不變。旋轉平面是 zw 平面,該平面上的點旋轉角度 θ。一般點僅在 zw 平面內旋轉,即僅更改其 z 和 w 座標來繞 xy 平面旋轉。
在二維和三維,所有旋轉都是簡單旋轉,因為只有一個旋轉平面。只有在四維以上才存在不是簡單旋轉的旋轉。在四維也存在雙重旋轉和等斜旋轉。
雙重旋轉
[编辑]雙旋轉有兩個旋轉平面,沒有固定平面,唯一的固定點是原點。旋轉發生在兩旋轉平面中。這些平面是正交的,也就是說,它們沒有共同的向量,因此一個平面中的每個向量都與另一個平面中的每個向量成直角。兩個旋轉平面跨越四維空間,因此空間中的每個點都可以由兩個點指定,每個平面上一個。
雙旋轉有兩個旋轉角度,每個旋轉平面一個。雙重旋轉有兩個平面和兩個非零角度α、β(如果任一角度為零,則是簡單旋轉)。第一個平面的旋轉α點,第二個平面的旋轉β點。所有其他點都旋轉α和β之間的角度,因此在某種意義上是αβ共同決定了旋轉量。對於一般的雙旋轉,旋轉平面和角度是唯一的,並且給定一般的旋轉,它們可以被計算。例如,xy 平面中的 α 和 zw 平面中的 β 的旋轉由矩陣給出
等斜旋轉
[编辑]
雙旋轉的一個特殊情況是角度相等,即 α = β ≠ 0。
例如,在等斜旋轉中所有非零點都會旋轉相同的角度 α。最重要的是,旋轉平面不是唯一標識的。相反,有無數對正交平面可以被視為旋轉平面。例如可以任意一點,它旋轉所在的平面以及與其正交的平面可以當作兩個旋轉平面。[8]
高維
[编辑]旋轉平面數量公式:
因此,超過四個維度,複雜性會迅速增加,並且如上所述對旋轉進行分類變得過於複雜而不實用,但可以進行一些觀察。
簡單旋轉可以在所有維度上被識別為僅具有一個旋轉平面的旋轉。 n 維的簡單旋轉圍繞會與旋轉平面正交的 (n − 2) 維子空間(即距其固定距離)發生。
A general rotation is not simple, and has the maximum number of planes of rotation as given above. In the general case the angles of rotations in these planes are distinct and the planes are uniquely defined. If any of the angles are the same then the planes are not unique, as in four dimensions with an isoclinic rotation.
In even dimensions (n = 2, 4, 6...) there are up to n/2 planes of rotation span the space, so a general rotation rotates all points except the origin which is the only fixed point. In odd dimensions (n = 3, 5, 7, ...) there are n − 1/2 planes and angles of rotation, the same as the even dimension one lower. These do not span the space, but leave a line which does not rotate – like the axis of rotation in three dimensions, except rotations do not take place about this line but in multiple planes orthogonal to it.[1]
數學性質
[编辑]The examples given above were chosen to be clear and simple examples of rotations, with planes generally parallel to the coordinate axes in three and four dimensions. But this is not generally the case: planes are not usually parallel to the axes, and the matrices cannot simply be written down. In all dimensions the rotations are fully described by the planes of rotation and their associated angles, so it is useful to be able to determine them, or at least find ways to describe them mathematically.
反射
[编辑]
Every simple rotation can be generated by two reflections. Reflections can be specified in n dimensions by giving an (n − 1)-dimensional subspace to reflect in, so a two-dimensional reflection is in a line, a three-dimensional reflection is in a plane, and so on. But this becomes increasingly difficult to apply in higher dimensions, so it is better to use vectors instead, as follows.
A reflection in n dimensions is specified by a vector perpendicular to the (n − 1)-dimensional subspace. To generate simple rotations only reflections that fix the origin are needed, so the vector does not have a position, just direction. It does also not matter which way it is facing: it can be replaced with its negative without changing the result. Similarly unit vectors can be used to simplify the calculations.
So the reflection in a (n − 1)-dimensional space is given by the unit vector perpendicular to it, m, thus:
where the product is the geometric product from geometric algebra.
If x′ is reflected in another, distinct, (n − 1)-dimensional space, described by a unit vector n perpendicular to it, the result is
This is a simple rotation in n dimensions, through twice the angle between the subspaces, which is also the angle between the vectors m and n. It can be checked using geometric algebra that this is a rotation, and that it rotates all vectors as expected.
The quantity mn is a rotor, and nm is its inverse as
So the rotation can be written
where R = mn is the rotor.
The plane of rotation is the plane containing m and n, which must be distinct otherwise the reflections are the same and no rotation takes place. As either vector can be replaced by its negative the angle between them can always be acute, or at most π/2. The rotation is through twice the angle between the vectors, up to π or a half-turn. The sense of the rotation is to rotate from m towards n: the geometric product is not commutative so the product nm is the inverse rotation, with sense from n to m.
Conversely all simple rotations can be generated this way, with two reflections, by two unit vectors in the plane of rotation separated by half the desired angle of rotation. These can be composed to produce more general rotations, using up to n reflections if the dimension n is even, n − 2 if n is odd, by choosing pairs of reflections given by two vectors in each plane of rotation.[9][10]
二重向量
[编辑]二重向量s are quantities from geometric algebra, clifford algebra and the exterior algebra, which generalise the idea of vectors into two dimensions. As vectors are to lines, so are bivectors to planes. So every plane (in any dimension) can be associated with a bivector, and every simple bivector is associated with a plane. This makes them a good fit for describing planes of rotation.
Every rotation plane in a rotation has a simple bivector associated with it. This is parallel to the plane and has magnitude equal to the angle of rotation in the plane. These bivectors are summed to produce a single, generally non-simple, bivector for the whole rotation. This can generate a rotor through the exponential map, which can be used to rotate an object.
Bivectors are related to rotors through the exponential map (which applied to bivectors generates rotors and rotations using 棣莫弗公式). In particular given any bivector B the rotor associated with it is
This is a simple rotation if the bivector is simple, a more general rotation otherwise. When squared,
it gives a rotor that rotates through twice the angle. If B is simple then this is the same rotation as is generated by two reflections, as the product mn gives a rotation through twice the angle between the vectors. These can be equated,
from which it follows that the bivector associated with the plane of rotation containing m and n that rotates m to n is
This is a simple bivector, associated with the simple rotation described. More general rotations in four or more dimensions are associated with sums of simple bivectors, one for each plane of rotation, calculated as above.
Examples include the two rotations in four dimensions given above. The simple rotation in the zw-plane by an angle θ has bivector e34θ, a simple bivector. The double rotation by α and β in the xy-plane and zw-planes has bivector e12α + e34β, the sum of two simple bivectors e12α and e34β which are parallel to the two planes of rotation and have magnitudes equal to the angles of rotation.
Given a rotor the bivector associated with it can be recovered by taking the logarithm of the rotor, which can then be split into simple bivectors to determine the planes of rotation, although in practice for all but the simplest of cases this may be impractical. But given the simple bivectors geometric algebra is a useful tool for studying planes of rotation using algebra like the above.[1][11]
特徵值和特徵平面
[编辑]The planes of rotations for a particular rotation using the eigenvalues. Given a general rotation matrix in n dimensions its characteristic equation has either one (in odd dimensions) or zero (in even dimensions) real roots. The other roots are in complex conjugate pairs, exactly
such pairs. These correspond to the planes of rotation, the eigenplanes of the matrix, which can be calculated using algebraic techniques. In addition arguments of the complex roots are the magnitudes of the bivectors associated with the planes of rotations. The form of the characteristic equation is related to the planes, making it possible to relate its algebraic properties like repeated roots to the bivectors, where repeated bivector magnitudes have particular geometric interpretations.[1][12]
另見
[编辑]註
[编辑]- ^ 1.0 1.1 1.2 1.3 1.4 Lounesto (2001) pp. 222–223
- ^ Lounesto (2001) p. 38
- ^ Hestenes (1999) p. 48
- ^ Lounesto (2001) p. 222
- ^ Lounesto (2001) p.87
- ^ Lounesto (2001) pp.27–28
- ^ Hestenes (1999) pp 280–284
- ^ Lounesto (2001) pp. 83–89
- ^ Lounesto (2001) p. 57–58
- ^ Hestenes (1999) p. 278–280
- ^ Dorst, Doran, Lasenby (2002) pp. 79–89
- ^ Dorst, Doran, Lasenby (2002) pp. 145–154
參考
[编辑]- Hestenes, David. New Foundations for Classical Mechanics 2nd. Kluwer. 1999. ISBN 0-7923-5302-1.
- Lounesto, Pertti. Clifford algebras and spinors. Cambridge: Cambridge University Press. 2001. ISBN 978-0-521-00551-7.[失效連結]
- Dorst, Leo; Doran, Chris; Lasenby, Joan. Applications of geometric algebra in computer science and engineering. Birkhäuser. 2002. ISBN 0-8176-4267-6.





















