主题:几何学
外观
几何学

几何学出现于处理空间关系的知识领域。几何学是前现代数学的两个领域之一,另一个是数字的研究。
在近代,几何学概念已经被扩展。它们有时显示高水平的抽象和复杂性。几何学现在使用微积分学和抽象代数的方法,从而使该领域的许多现代分支不容易被辨认出是早期几何学的后代(见数学领域)。工作于或者是专业从事于几何学的人是几何学家。
特色条目
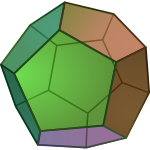
在幾何學中,正圖形又稱正多胞形(英語:Regular polytope),即正幾何圖形,是一種對稱性对于標記可递的幾何體,且具有高度對稱性,對於該幾何體內所有同維度的元素(如:點、線、面)都完全具有相同的性質,並且每一個元素皆為一個正圖形,例如,正方體所有的面的面積及形狀皆相同,且皆為正方形,是一個二維正多胞形、所有邊的長度也相同,所有角的角度及形式也相同,因此正方體是一個正圖形或正多胞形。對於所有元素,或叫j維面(對所有的 0 ≤ j ≤ n,其中n是該幾何體所在的維度) — 胞、面等等 — 也都对于多胞形的对称性可递,也是≤ n维的正圖形。
正图形是正多边形(例如,正方形或者正五边形)和正多面体(例如立方体)的向任意维度的推广类比。正图形极强的对称性使它们拥有极强的审美价值,吸引着数学家和数学爱好者。
一般地,n维正图形被定义为有正维面[(n − 1)-表面]和正顶点图。这两个条件已经能充分地保证所有面、所有顶点都是相似的。但要注意的是,这一定义并不适用于抽象多胞形。
一个正图形能用形式为{a, b, c, ...., y, z}的施莱夫利符号代表,其正的面为{a, b, c, ..., y},顶点图为{b, c, ..., y, z}。
相关专题
欢迎参与

- 欢迎改进或扩充的条目 :
- 请求条目:
- 栏目特色图片, 和精选传记
- 几何学纲要、几何学历史、合成几何学、几何学议题列表、广义三角函数
- 超矩形、手性 (数学)、伪三角形、抽象多胞形,考克斯特符号、考克斯特元素、421多胞形、E8、锥面、一萬邊形
- 凸幾何、轉換幾何、代數曲面、Gröbner基、實代數幾何、複幾何
- 模板: Template:Honeycombs、Template:Tessellation、Template:Mathematics and art(数学和艺术)
- 需要继续扩充或翻译的条目:
- 需要专家关注
- 張量(tensor)
你知道吗?
分类
以下的分类树显示Category:几何学下的分类。